Heirarchy of Sequencing Type Classes

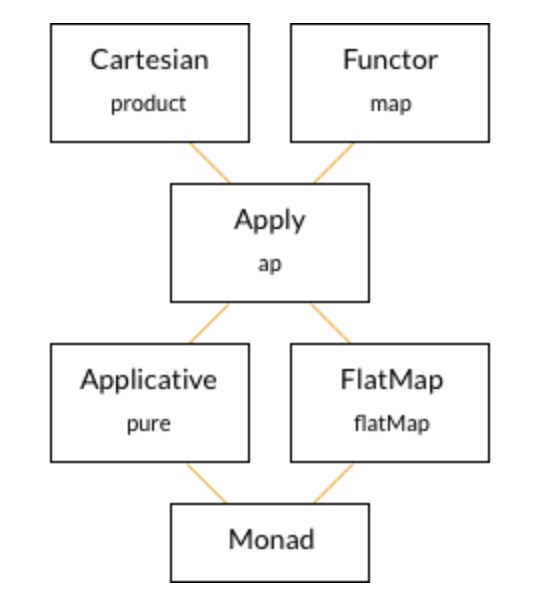
(See also this nice infographic)

Each type classes represents:

• represents a set of sequencing semantics
• represents a set of charateristic methods
• defines the functionality of its supertypes in terms of them

The inheritance relationships are constant across all instances of a type class.

• Apply defines product in terms of ap and map
• Monad defines product, ap, and map in terms of pure and flatMap.

trait Monad[F[_]] extends Applicative[F] with FlatMap[F] {
    def pure[A](a: A): F[A]

    def flatMap[A, B](value: F[A])(func: A => F[B]): F[B]

    def map[A, B](value: F[A])(func: A => B): F[B] =
        flatMap(value)(a => pure(func(a)))

    def ap[A, B](ff: F[A => B])(fa: F[A]): F[B] =
}

For example, let's say we have two data types:

• Foo is a monad. It has an instance of Monad type class that implements pure and flatMap. ap, product, and map are the inherited standard definitions.
• Bar is an applicative functor. It has an instance of Applicative that implements pure and ap. product and map are inherited standard definitions.

We know more about Foo than Bar. Monad is a subtype of Applicative, so we can guarantee the all the properties of Bar for Foo as well. But Foo has another property we can guarantee (i.e. flatMap) that we cannot guarantee with Bar. On the other hand, we know that Bar may have wider range of behaviors than Foo, since it doesn't have to follow laws brought it by flatMap.

This is a trade off of power versus constraint. The more constraints, the better known behaviors, the fewer behavior it can model.

Monads can serve a lot of behaviors while providing good guarantees about those behaviors. Sometimes, though, it may not be right for the job.

Monads provide strict sequencing, applicatives and semigroupals do not. We can use the latter for parallel/independent computations that monads cannot do.